排序算法总结

简介

刷leetcode碰到一个难题，里面用到了分治法，想到了归并排序，觉得以前学的排序基本忘得差不多了，特别是快排，直接sort()调用，自己基本实现不了，索性重新复习一遍

归并排序

简介

归并排序(Merging Sort)就是将两个或两个以上的有序表合并成一个有序表的过程。将两个有序表合并成一个有序表的过程称为2-路归并，2-路归并最为简单和常用。该算法是采用分治法（Divide and Conquer）的一个非常典型的应用。

算法思想

假设初始序列含有n个记录，则可以看成是n个有序的子序列，每个子序列的长度是１，然后两两归并，得到[n/2]个长度为2或１的有序子序列；再两两归并,…如此重复，直到得到一个长度为n的有序子序列为止。

用途

1.排序：归并排序的时间复杂度是O(nlog2n)，当有n个记录时，需要进行log2n次归并排序，每一次归并，关键字比较次数不超过n，元素移动次数都是n，因此是nlog2n。
归并排序是稳定排序(在原序列中，r[i]=r[j]，且r[i]在r[j]之前，而在排序后的序列中，r[i]仍在r[j]之前，则称这种排序算法是稳定的)，可以用于链式结构。
2.找逆序对数，以前打ACM碰到过好几次，第一次见到这种题觉得好难，这就说明对归并排序理解不深，这点在紫书上也提到过。当然也可以通过树状数组解决这类问题。

代码＋解释

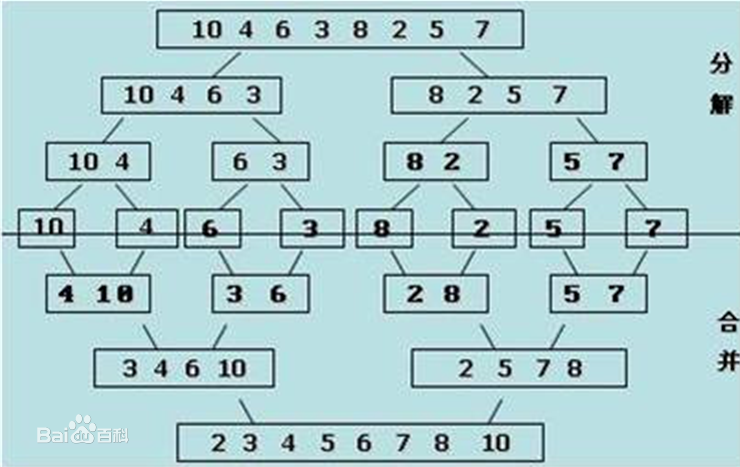
对于这张图，将原序列分解为n个子序列，然后开始比较归并，对于分解可以用二分＋递归来实现，合并也是一样。

//算法实现
//采用紫书代码
void merge_sort(int* A, int x, int y, int* T) {
    if(y - x > 1) {
        int m = x + (y - x) / 2;     //划分
	int p = x, q = m, i = x;    
	merge_sort(A, x, m, T);      //递归求解
	merge_sort(A, m, y, T);      //递归求解
	while(p < m || q < y) {
	    if(q >= y || (p < m && A[p] <= A[q])) T[i++] = A[p++];     //从左半数组复制到临时空间
	    else T[i++] = A[q++];                                      //从右半数组复制到临时空间
	　　　　// else T[i++] = A[q++], cnt += m - p;                     //这一行就可以实现求逆序对数的问题，其中cnt要先清零
	}
	for(i = x; i < y; i++) A[i] = T[i];                            //从辅助空间复制回A数组
    }
}

快速排序

简介

快速排序（Quick Sort）是对冒泡排序的一种改进。基本思想是：通过一趟排序将要排序的数据分割成独立的两部分，其中一部分的所有数据都比另外一部分的所有数据都要小，然后再按照此方法对这两部分数据分别进行快速排序，整个排序过程可以递归进行，以此达到整个数据变成有序序列。

算法思想

快速排序采用了分治法的思想，它的基本思想就是通过一趟排序将要排序的数据分割成独立的两部分，其中一部分的所有数据都比另外一部分的所有数据都要小，然后再按照此方法对这两部分数据分别进行快速排序，整个排序过程可以递归进行，以此达到整个数据变成有序序列。快速排序的实现过程如下：

选择一个基准元素（一般是第一个元素或者最后一个元素）；
将序列中所有比基准元素小的元素放在基准元素的前面，所有比基准元素大的元素放在基准元素的后面（相同的数可以放在任意一边）；
对左右两个分区重复以上步骤直到各区间只有一个元素。

用途

排序：快速排序算法的时间复杂度为O(nlogn)，平均情况下比冒泡排序、插入排序等常见的排序算法都要快得多。
查找第k大/小元素：通过快速排序算法可以快速地找出一个无序序列中第k大或第k小的元素，即找到一个元素，它的位置是从小到大排列的第k个或从大到小排列的第k个。

代码＋解释

void quicksort(int arr[], int left, int right) {
    int i, j, pivot, temp;
    if (left < right) {
        pivot = arr[right];
        i = left - 1;
        for (j = left; j < right; j++) {
            if (arr[j] < pivot) {
                i++;
                temp = arr[i];
                arr[i] = arr[j];
                arr[j] = temp;
            }
        }
        temp = arr[i+1];
        arr[i+1] = arr[right];
        arr[right] = temp;

        quicksort(arr, left, i);
        quicksort(arr, i+2, right);
    }
}

其中，arr 表示待排序的数组，left 表示数组的左边界，right 表示数组的右边界。在 partition 函数中，我们选择最后一个元素作为基准值，然后用 i 表示小于基准值的元素的最后一个下标，遍历数组中每一个元素，如果小于基准值，则将其交换到 i 的后面，最后再将基准值交换到 i 的后面，此时 i+1 就是基准值的位置。最后分别递归对左边和右边的子序列进行排序。